AGM - Advanced Topics in Normalizing Flows - 1x1 convolution¶
Introduction¶
The Glow, a flow-based generative model extends the previous invertible generative models, NICE and RealNVP, and simplifies the architecture by replacing the reverse permutation operation on the channel ordering with Invertible 1x1 Convolutions. Glow is famous for being the one of the first flow-based models that works on high resolution images and enables manipulation in latent space. Let’s have a look at the interactive demonstration from OpenAI.

Glow consists of a series of steps of flow. Each step of flow comprises Actnorm followed by an Invertible 1×1 Convolution, and finally a Coupling Layer.
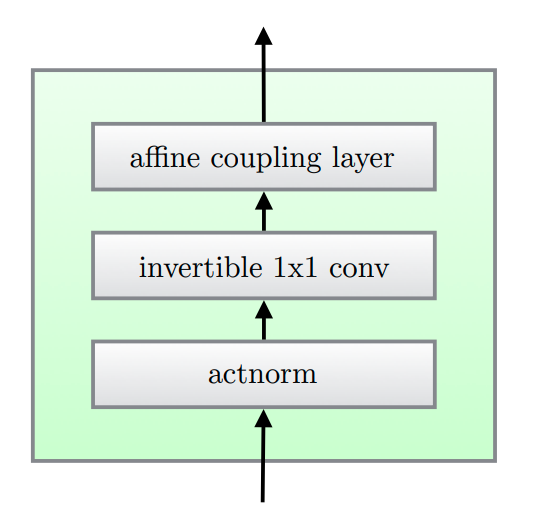
Actnorm performs an affine transformation with a scale and bias parameter per channel, similar to that of batch normalization, but works on mini-batch size 1. The statistics (mean and std), however, are only calculated once to initialize the scale and bias parameters.
Invertible 1×1 Convolution with equal number of input and output channels is a generalization of any permutation of the channel ordering. Recall the operation between layers of the RealNVP flow, the ordering of channels is switched so that all the data dimensions have a chance to be mixed. 1x1 convolution is proposed to replace this fixed permutation with a learned invertible operation.
Coupling Layer is a powerful reversible transformation where the forward function, the reverse function and the logdeterminant are computationally efficient. The design is the same as in RealNVP.

In this tutorial, we will be focusing on the implementation of invertible 1x1 convolution layer.
Invertible 1x1 convolution¶
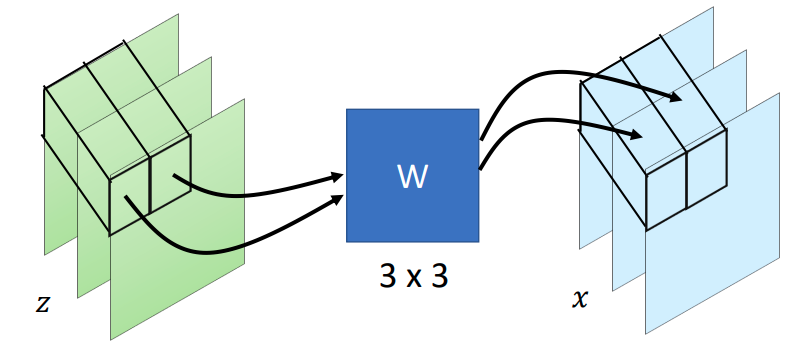
Given an input of shape \(H\times W\times C\) applied with a 1x1 convolution with \(C\) filters, meaning the output tensor shape is also going to be \(H\times W\times C\). Thus, each layer has a set of weights \(W\) with \(C\times C\) values. The forward operation acts just like a typical convolution, while the inverse operation can be computed by simply applying a convolution with \(W^{-1}\) weights.
Enough descriptions! Now let’s take a look at the code.
[14]:
import torch
from torch import nn
from torch.nn import functional as F
class InvConv2d(nn.Module):
def __init__(self, in_channel):
super().__init__()
weight = torch.randn(in_channel, in_channel)
# use the Q matrix from QR decomposition as the initial weight to make sure it's invertible
q, _ = torch.qr(weight)
weight = q.unsqueeze(2).unsqueeze(3)
self.weight = nn.Parameter(weight)
def forward(self, input, logdet, reverse=False):
_, _, height, width = input.shape
# You can also use torch.slogdet(self.weight)[1] to summarize the operations below\n",
dlogdet = (
height * width * torch.log(torch.abs(torch.det(self.weight.squeeze())))
)
if not reverse:
out = F.conv2d(input, self.weight)
logdet = logdet + dlogdet
else:
out = F.conv2d(input, self.weight.squeeze().inverse().unsqueeze(2).unsqueeze(3))
logdet = logdet - dlogdet
return out, logdet
Note that to calculate the determinant of \(W\) could be computationally expensive, thus there’s also an implementation which utilizes LU decomposition to speed up, as suggested in the Glow paper.
The idea is to parameterizing \(W\) directly in its LU decomposition:
where \(P\) is a permutation matrix, \(L\) is a lower triangular matrix with ones on the diagonal, \(U\) is an upper triangular matrix with zeros on the diagonal, and \(s\) is a vector.
The log-determinant is then simply:
Please check out the link above for the implementation.
A small pitfall¶
As you might notice, there’s an inverse operation for the weight \(W\) involved when the 1x1 convolution is forwarding reversely. As a result, an error can occur when the weight \(W\) is not invertible, even though it seldom happens.
To our best knowledge, there’s no elegant solution to address this, but an easy way to workaround: If this happens unfortunately during the training, one can try to restart from the recent checkpoint.
A complete flow block¶
Now we have the Invertible 1x1 Convolution. Together with the aforementioned Actnorm and Coupling Layer, we are ready to try out the power of the Glow by plugging the block into the model we had in the NFs tutorial!
[21]:
class ActNorm(nn.Module):
def __init__(self, in_channel):
super().__init__()
self.loc = nn.Parameter(torch.zeros(1, in_channel, 1, 1))
self.log_scale = nn.Parameter(torch.zeros(1, in_channel, 1, 1))
self.register_buffer("initialized", torch.tensor(0, dtype=torch.uint8))
def initialize(self, input):
with torch.no_grad():
flatten = input.permute(1, 0, 2, 3).contiguous().view(input.shape[1], -1)
mean = (
flatten.mean(1)
.unsqueeze(1)
.unsqueeze(2)
.unsqueeze(3)
.permute(1, 0, 2, 3)
)
std = (
flatten.std(1)
.unsqueeze(1)
.unsqueeze(2)
.unsqueeze(3)
.permute(1, 0, 2, 3)
)
self.loc.data.copy_(-mean)
self.log_scale.data.copy_(-std.clamp_(min=1e-6).log())
def forward(self, input, logdet, reverse=False):
_, _, height, width = input.shape
if self.initialized.item() == 0:
self.initialize(input)
self.initialized.fill_(1)
dlogdet = height * width * torch.sum(self.log_scale)
if not reverse:
logdet += dlogdet
return self.log_scale.exp() * (input + self.loc), logdet
else:
dlogdet *= -1
logdet += dlogdet
return input / self.log_scale.exp() - self.loc, logdet
A sample code for Actnorm is provided above.
As for Coupling Layer, please refer to the one in the NFs tutorial.
Conclusion¶
We’ve learned an advanced flow-based layer from the Glow model, an Invertible 1x1 convolution, which is adapted from the typical 1x1 convolution layers.
